下面的定义与图,都适合任何周期的 K 线图。先看下图,图中的小线段代表的是 K线,这里不分阳线阴线,只看 K 线的高低点。
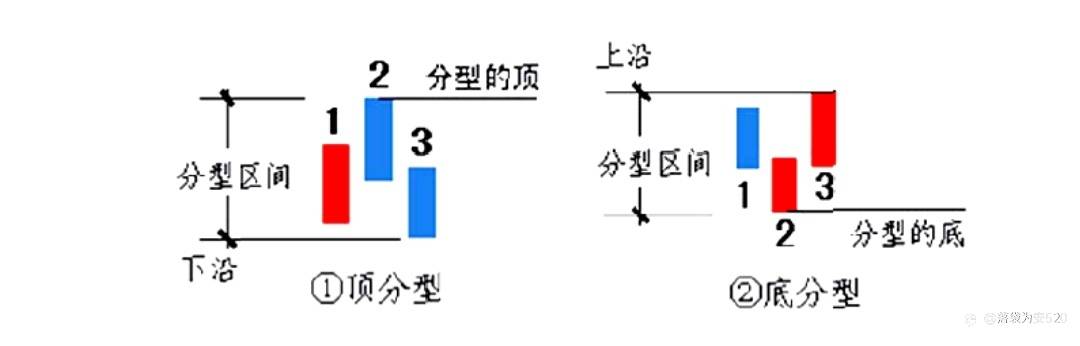
如图 1 所示,第二 K 线高点是相邻三 K 线高点中最高的,而低点也是相邻三 K 线低点中最高的,本理论给一个定义叫顶分型;如图 2 所示,第二 K 线低点是相邻三 K 线低点中最低的,而高点也是相邻三 K 线高点中最低的,本理论给一个定义叫底分型。看不明白定义的看图就明白了,图形更直观。
顶分型的最高点叫该分型的顶,底分型的最低点叫该分型的底,由于顶分型的底和底分型的顶是没有意义的,所以顶分型的顶和底分型的底就可以简称为顶和低。也就是说,当我们以后说顶和底时,就分别是说顶分型的顶和底分型的底。在实际图形里,对于分型,最大的麻烦就是前后K线间的包含关系,如图3所示,所谓的包含关系就是一K线的高低点全在另一K线的范围里。

这种情况下,可以这样处理,在向上时,把两K线的最高点当高点,而两K线低点中的较高者当成低点,这样就把两K线合并成一新的K线;反之当向下时,把两K线的最低点当低点,而两K线高点中的较低者当成高点,这样就把两K线合并成一新的K线。经过这样的处理,所有K线图都可以处理成没有包含关系的图形。
上面说向上、向下,那什么是向上?什么是向下?其实这根本没什么可说的,任何看过图的都知道什么是向上,什么是向下。
假设第n根K线满足第n根与第n 1根的包含关系,而第n根与第n-1根不是包含关系,那么,如果gn>=gn-1,那么就称第 n-1、n、n 1根K线是向上的;如果 dn<=dn-1,那么就称第n-1、n、n 1根K线是向下的。

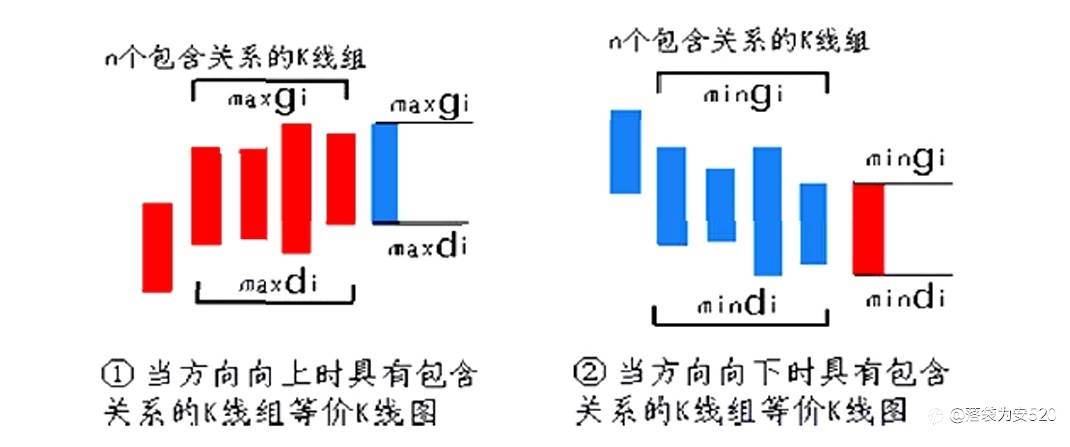
根据上面的方法,用[di,gi]记号第i根K线的最低和最高构成的区间,当向上时,顺次 n 个包含关系的K 线组,等价于[maxdi,maxgi]的区间对应的 K 线,也就是说,这 n个K 线,和最低最高的区间为[maxdi,maxgi]的 K 线是一回事情;向下时,顺次 n 个包含关系的K线组,等价于[mindi,mingi]的区间对应的K线。

Đã chỉnh sửa 17 Feb 2021, 15:13
Tuyên bố miễn trừ trách nhiệm: Quan điểm được trình bày hoàn toàn là của tác giả và không đại diện cho quan điểm chính thức của Followme. Followme không chịu trách nhiệm về tính chính xác, đầy đủ hoặc độ tin cậy của thông tin được cung cấp và không chịu trách nhiệm cho bất kỳ hành động nào được thực hiện dựa trên nội dung, trừ khi được nêu rõ bằng văn bản.

Để lại tin nhắn của bạn ngay bây giờ